Noções introdutórias de matemática nos First Person Shooters

A matemática está presente em vários momentos de nossas  vidas. Desde o momento que acordamos e temos que pensar quantos minutos faltam para as 8 da manhã, passando por quanto podemos gastar no mercado e até mesmo nas teorias números da loteria.

No desenvolvimento de jogos de vídeo-game a coisa anda no mesmo caminho. Se você for observar os três principais nichos de jogos, todos eles têm a matemática envolvida de alguma forma.

Quais seriam esses três? FPS, que trataremos neste artigo, Estratégia e Simulação.

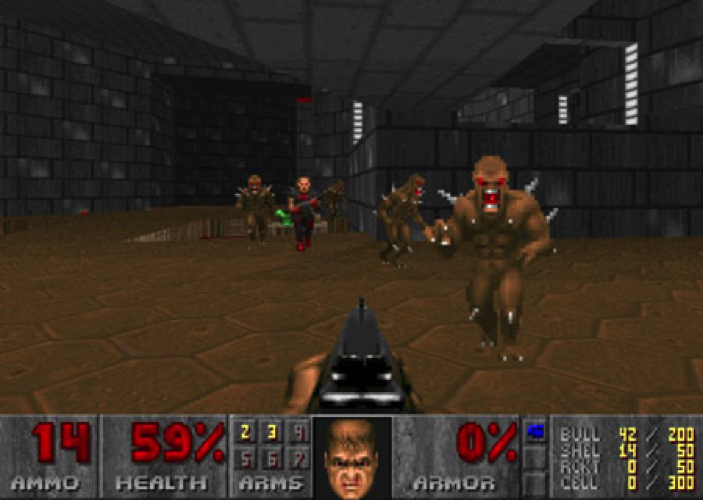
O chamado first person shooter é aquele tipo de jogo que você transita por levels em 3D e nos quais você carrega uma arma com a qual mata os inimigos. Essa é a definição mais clássica e que faz vir à mente jogos como Doom e Goldeneye – ambos paradigmas no gênero. Como a matemática está inserida neles? Bom, da definição dos mesmos, a gente chega a conclusões. O principal ramo da matemática empregado nos FPS é a geometria espacial – planos, balística e construção de elementos com altura, largura e, principalmente, profundidade. Além disso, o conceito físico principal é o ponto de referência em relação a outros planos. Até porque estamos falando da “primeira pessoa”. A descrição matemática é mais ou menos assim: Criar um mundo de maneira que esse mundo seria visto por alguém dentro deste mundo, sendo este o ponto de referência na construção do meio ao seu redor – e as interações do meio com esse “ponto de referência”.

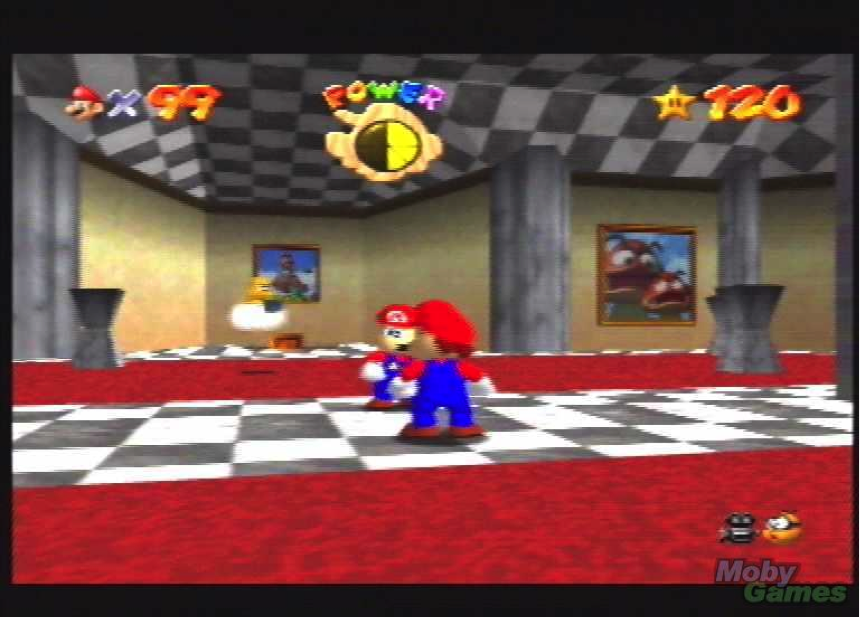
Lógico, essa é apenas a noção introdutória. É importante lembrar, também, que existem os chamados jogos em “terceira pessoa”. Exemplo clássico do gênero – e paradigma – é Super Mario 64. Nele, a nuvem Lakitu filma Mario durante sua caça às 120 estrelas para salvar a Princesa Peach. Ou seja: o ponto de referência principal é Mario. O ponto de referência secundário – o cameraman – era Lakitu. O que tínhamos aqui? Simples, é só adotar a teoria exposta acima. Mario interage com o meio e Lakitu interage com o jogador quando é necessário adotar um outro ponto de referência no eixo x/y/z para acompanhar a interação de Mario com o meio.

O bojo é, então, simples: tudo é ponto de referência, planos e geometria espacial. Jogar Goldeneye parece simples em 1997 – mas você, quando criança, nunca imaginou que mesmo em linguagem simples, a matemática estaria tão presente.